Metódy riešenia limitov. Neistoty Poradie rastu funkcie

Derivácia funkcie nespadá ďaleko a v prípade L'Hopitalových pravidiel spadá presne tam, kde spadá pôvodná funkcia. Táto okolnosť pomáha pri odhaľovaní neistôt tvaru 0/0 alebo ∞/∞ a niektorých ďalších neistôt vznikajúcich pri výpočte limit pomer dvoch nekonečne malých alebo nekonečne veľkých funkcií. Toto pravidlo značne zjednodušuje výpočet (v skutočnosti dve pravidlá a poznámky k nim):

Ako ukazuje vzorec vyššie, pri výpočte limity pomeru dvoch nekonečne malých alebo nekonečne veľkých funkcií možno limitu pomeru dvoch funkcií nahradiť limitou pomeru ich funkcií. deriváty a tak získať určitý výsledok.

Prejdime k presnejším formuláciám L'Hopitalových pravidiel.

L'Hopitalovo pravidlo pre prípad hranice dvoch nekonečne malých hodnôt. Nechajte funkcie f(X) a g(X a. A v samom bode a a derivácia funkcie g(X) sa nerovná nule ( g"(X a sa navzájom rovnajú a rovnajú sa nule:

.

L'Hôpitalovo pravidlo pre prípad hranice dvoch nekonečne veľkých veličín. Nechajte funkcie f(X) a g(X) majú derivácie (to znamená, že sú diferencovateľné) v niektorom okolí bodu a. A v samom bode a môžu alebo nemusia mať deriváty. Navyše v okolí bodu a derivácia funkcie g(X) sa nerovná nule ( g"(X)≠0 ) a limity týchto funkcií, keďže x smeruje k hodnote funkcie v bode a sa navzájom rovnajú a rovnajú sa nekonečnu:

.

Potom sa limita pomeru týchto funkcií rovná limite pomeru ich derivácií:

Inými slovami, pre neistoty tvaru 0/0 alebo ∞/∞ sa limita pomeru dvoch funkcií rovná limite pomeru ich derivácií, ak druhá existuje (konečná, to znamená rovná a určitý počet alebo nekonečno, to znamená, že sa rovná nekonečnu).

Poznámky.

1. Pravidlá spoločnosti L'Hopital sa vzťahujú aj na funkcie f(X) a g(X) nie sú definované na X = a.

2. Ak pri výpočte limity podielu derivácií funkcií f(X) a g(X) opäť sa dostávame k neurčitosti tvaru 0/0 alebo ∞/∞, potom by sa L'Hopitalove pravidlá mali aplikovať opakovane (aspoň dvakrát).

3. L'Hopitalove pravidlá sú použiteľné aj vtedy, keď argument funkcií (x) smeruje k nekonečnému číslu a a do nekonečna ( X → ∞).

Neistoty iných typov možno redukovať aj na neistoty typov 0/0 a ∞/∞.

Zverejnenie neistôt typu "nula delená nulou" a "nekonečno delené nekonečnom"

Príklad 1

X=2 vedie k neurčitosti tvaru 0/0. Preto derivácia každej funkcie a dostaneme

V čitateli sa vypočítala derivácia polynómu a v menovateli - derivácia komplexnej logaritmickej funkcie. Pred posledným znakom rovnosti, obvyklý limit, nahradenie dvojky namiesto x.

Príklad 2 Vypočítajte limitu pomeru dvoch funkcií pomocou L'Hospitalovho pravidla:

Riešenie. Substitúcia do danej hodnotovej funkcie X

Príklad 3 Vypočítajte limitu pomeru dvoch funkcií pomocou L'Hospitalovho pravidla:

Riešenie. Substitúcia do danej hodnotovej funkcie X=0 vedie k neurčitosti tvaru 0/0. Preto vypočítame derivácie funkcií v čitateli a menovateli a dostaneme:

Príklad 4 Vypočítajte

Riešenie. Dosadenie hodnoty x rovnej plus nekonečnu do danej funkcie vedie k neurčitosti tvaru ∞/∞. Preto aplikujeme L'Hopitalovo pravidlo:

Komentujte. Prejdime k príkladom, v ktorých sa L'Hopitalovo pravidlo musí aplikovať dvakrát, teda dostať sa na hranicu pomeru druhých derivácií, keďže limita pomeru prvých derivácií je neurčitosťou tvaru 0/0 alebo ∞/∞.

Zverejnenie neistôt tvaru "nula násobená nekonečnom"

Príklad 12. Vypočítajte

.

Riešenie. Dostaneme

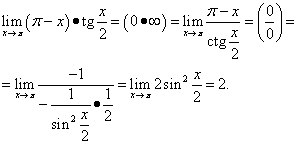
Tento príklad používa trigonometrickú identitu.

Zverejnenie neistôt typu "nula na mocninu nuly", "nekonečno na mocninu nuly" a "jedna na mocninu nekonečna"

Neistoty tvaru alebo sa zvyčajne redukujú na tvar 0/0 alebo ∞/∞ pomocou logaritmu funkcie tvaru

Na výpočet limitu výrazu by sme mali použiť logaritmickú identitu, ktorej špeciálnym prípadom je vlastnosť logaritmu .

Pomocou logaritmickej identity a vlastnosti kontinuity funkcie (aby sme prekročili znamienko limitu), limit by sa mal vypočítať takto:

Samostatne by sme mali nájsť limit výrazu v exponente a zostave e do zisteného stupňa.

Príklad 13

Riešenie. Dostaneme

.

.

Príklad 14 Vypočítajte pomocou L'Hopitalovho pravidla

Riešenie. Dostaneme

Vypočítajte limitu výrazu v exponente

.

.

Príklad 15 Vypočítajte pomocou L'Hopitalovho pravidla

Mnoho ľudí sa veľmi často pýta, prečo nie je možné použiť delenie nulou? V tomto článku sa budeme veľmi podrobne zaoberať tým, odkiaľ toto pravidlo pochádza, ako aj to, aké akcie možno vykonať s nulou.

V kontakte s

Nula sa dá nazvať jedným z najzaujímavejších čísel. Toto číslo nemá žiadny význam, znamená prázdnotu v pravom zmysle slova. Ak však vedľa ľubovoľnej číslice umiestnite nulu, hodnota tejto číslice sa niekoľkonásobne zväčší.

Číslo je samo o sebe veľmi záhadné. Používali ho starí Mayovia. Pre Mayov znamenala nula „začiatok“ a od nuly začínalo aj odpočítavanie kalendárnych dní.

Veľmi zaujímavým faktom je, že znak nuly a znak neistoty boli pre nich podobné. Mayovia tým chceli ukázať, že nula je rovnaký identický znak ako neistota. V Európe sa označenie nula objavilo pomerne nedávno.

Tiež veľa ľudí pozná zákaz spojený s nulou. To povie každý nemožno deliť nulou. Vravia to učitelia v škole a deti to väčšinou berú za slovo. Zvyčajne deti buď jednoducho nemajú záujem to vedieť, alebo vedia, čo sa stane, ak sa po vypočutí dôležitého zákazu okamžite spýtajú: „Prečo nemôžete deliť nulou? Ale keď starnete, záujem sa prebúdza a chcete vedieť viac o dôvodoch takéhoto zákazu. Existujú však rozumné dôkazy.

Akcie s nulou

Najprv musíte určiť, aké akcie možno vykonať s nulou. Existuje viacero druhov aktivít:

• Pridanie;
• Násobenie;
• Odčítanie;
• Delenie (nula číslom);
• Umocňovanie.

Dôležité! Ak sa k akémukoľvek číslu počas sčítania pridá nula, potom toto číslo zostane rovnaké a nezmení svoju číselnú hodnotu. To isté sa stane, ak od ľubovoľného čísla odčítate nulu.

S násobením a delením je to trochu inak. Ak vynásobte ľubovoľné číslo nulou, potom sa súčin tiež stane nulou.

Zvážte príklad:

Napíšme to ako dodatok:

Celkovo je tam päť pridaných núl, takže sa to ukazuje

Skúsme vynásobiť jedna nulou. Výsledok bude tiež nulový.

Nulu možno deliť aj iným číslom, ktoré sa jej nerovná. V tomto prípade sa ukáže, ktorého hodnota bude tiež nulová. Rovnaké pravidlo platí pre záporné čísla. Ak vydelíte nulu záporným číslom, dostanete nulu.

Môžete tiež zvýšiť ľubovoľné číslo na nulový výkon. V tomto prípade dostanete 1. Je dôležité si uvedomiť, že výraz „nula k nule“ je absolútne nezmyselný. Ak sa pokúsite zvýšiť nulu na akúkoľvek moc, dostanete nulu. Príklad:

Použijeme pravidlo násobenia, dostaneme 0.

Je možné deliť nulou

Takže tu sa dostávame k hlavnej otázke. Je možné deliť nulou všeobecne? A prečo nie je možné deliť číslo nulou, keďže všetky ostatné operácie s nulou plne existujú a platia? Ak chcete odpovedať na túto otázku, musíte sa obrátiť na vyššiu matematiku.

Začnime s definíciou pojmu, čo je nula? Učitelia škôl tvrdia, že nula je nič. Prázdnota. To znamená, že keď poviete, že máte 0 pier, znamená to, že nemáte žiadne perá.

Vo vyššej matematike je pojem „nula“ širší. Vôbec to neznamená prázdne. Tu sa nule hovorí neistota, pretože ak si urobíte malý prieskum, ukáže sa, že delením nuly nulou môžeme vo výsledku dostať akékoľvek iné číslo, ktoré nemusí byť nevyhnutne nula.

Viete, že tie jednoduché aritmetické operácie, ktoré ste študovali v škole, nie sú medzi sebou také rovné? Najzákladnejšie kroky sú sčítanie a násobenie.

Pre matematikov pojmy „“ a „odčítanie“ neexistujú. Predpokladajme: ak sa tri odpočítajú od piatich, zostanú dve. Takto vyzerá odčítanie. Matematici by to však napísali takto:

Ukazuje sa teda, že neznámy rozdiel je určité číslo, ktoré je potrebné pridať k 3, aby ste dostali 5. To znamená, že nemusíte nič odčítať, stačí nájsť vhodné číslo. Toto pravidlo platí pre sčítanie.

Veci sú trochu iné s pravidlá násobenia a delenia. Je známe, že násobenie nulou vedie k nulovému výsledku. Napríklad, ak 3:0=x, potom ak otočíte záznam, dostanete 3*x=0. A číslo, ktoré sa vynásobí 0, dá v súčine nulu. Ukazuje sa, že číslo, ktoré by v súčine s nulou dávalo inú hodnotu ako nula, neexistuje. To znamená, že delenie nulou nemá zmysel, to znamená, že vyhovuje nášmu pravidlu.

Čo sa však stane, ak sa pokúsite rozdeliť nulu samotnú? Vezmime x ako nejaké neurčité číslo. Ukazuje sa rovnica 0 * x \u003d 0. Dá sa to vyriešiť.

Ak sa pokúsime vziať nulu namiesto x, dostaneme 0:0=0. Zdalo by sa to logické? Ale ak sa pokúsime vziať akékoľvek iné číslo namiesto x, napríklad 1, skončíme s 0:0=1. Rovnaká situácia nastane, ak si vezmete akékoľvek iné číslo a zapoj to do rovnice.

V tomto prípade sa ukazuje, že ako faktor môžeme vziať akékoľvek iné číslo. Výsledkom bude nekonečné množstvo rôznych čísel. Niekedy má predsa delenie 0 vo vyššej matematike zmysel, no vtedy väčšinou nastane určitá podmienka, vďaka ktorej si predsa len môžeme vybrať jedno vhodné číslo. Táto akcia sa nazýva „zverejnenie neistoty“. V bežnej aritmetike delenie nulou opäť stratí význam, pretože si nebudeme môcť vybrať žiadne jedno číslo z množiny.

Dôležité! Nula sa nedá deliť nulou.

Nula a nekonečno

Nekonečno je vo vyššej matematike veľmi bežné. Keďže pre školákov jednoducho nie je dôležité vedieť, že stále existujú matematické operácie s nekonečnom, učitelia nevedia deťom poriadne vysvetliť, prečo sa nulou deliť nedá.

Študenti sa začínajú učiť základné matematické tajomstvá až v prvom ročníku inštitútu. Vyššia matematika poskytuje veľký súbor problémov, ktoré nemajú riešenie. Najznámejšie problémy sú problémy s nekonečnom. Dajú sa vyriešiť pomocou matematická analýza.

Môžete tiež použiť na nekonečno základné matematické operácie: sčítanie, násobenie číslom. Bežne sa používa aj odčítanie a delenie, no nakoniec aj tak prídu na dve jednoduché operácie.

Ale čo bude ak skúsiš:

• Vynásobte nekonečno nulou. Teoreticky, ak sa pokúsime vynásobiť akékoľvek číslo nulou, dostaneme nulu. Ale nekonečno je neurčitá množina čísel. Keďže nemôžeme vybrať jedno číslo z tejto množiny, výraz ∞*0 nemá riešenie a je absolútne nezmyselný.
• Nula delená nekonečnom. Toto je rovnaký príbeh ako vyššie. Nemôžeme si vybrať jedno číslo, čo znamená, že nevieme, čím ich rozdeliť. Výraz nedáva zmysel.

Dôležité! Nekonečno je trochu iné ako neistota! Nekonečno je typ neistoty.

Teraz skúsme deliť nekonečno nulou. Zdalo by sa, že by mala existovať neistota. Ale ak sa pokúsime nahradiť delenie násobením, dostaneme veľmi jednoznačnú odpoveď.

Napríklad: ∞/0=∞*1/0= ∞*∞ = ∞.

Dopadá to takto matematický paradox.

Prečo sa nedá deliť nulou

Myšlienkový experiment, skúste deliť nulou

Záver

Takže teraz vieme, že nula podlieha takmer všetkým operáciám, ktoré sa vykonávajú, s výnimkou jednej jedinej. Nemôžete deliť nulou len preto, že výsledkom je neistota. Tiež sme sa naučili, ako operovať s nulou a nekonečnom. Výsledkom takýchto akcií bude neistota.

Číslo 0 môže byť reprezentované ako akási hranica oddeľujúca svet reálnych čísel od imaginárnych alebo záporných. Kvôli nejednoznačnej polohe sa mnohé operácie s touto číselnou hodnotou neriadia matematickou logikou. Nemožnosť delenia nulou je toho ukážkovým príkladom. A povolené aritmetické operácie s nulou možno vykonávať pomocou všeobecne akceptovaných definícií.

História nuly

Nula je referenčný bod vo všetkých štandardných číselných sústavách. Európania začali toto číslo používať relatívne nedávno, ale mudrci starovekej Indie používali nulu už tisíc rokov, kým toto prázdne číslo pravidelne používali európski matematici. Už pred Indmi bola nula povinnou hodnotou v mayskom číselnom systéme. Tento americký ľud používal dvanástnikový systém a prvý deň každého mesiaca začínal nulou. Zaujímavé je, že u Mayov sa znak pre „nulu“ úplne zhodoval so znakom pre „nekonečno“. Starí Mayovia teda dospeli k záveru, že tieto množstvá sú identické a nepoznateľné.

Matematické operácie s nulou

Štandardné matematické operácie s nulou možno zredukovať na niekoľko pravidiel.

Sčítanie: ak k ľubovoľnému číslu pridáte nulu, nezmení sa jeho hodnota (0+x=x).

Odčítanie: pri odčítaní nuly od ľubovoľného čísla zostáva hodnota odčítaného nezmenená (x-0=x).

Násobenie: akékoľvek číslo vynásobené 0 dáva v súčine 0 (a*0=0).

Delenie: Nulu možno deliť ľubovoľným nenulovým číslom. V tomto prípade bude hodnota takéhoto zlomku 0. A delenie nulou je zakázané.

Umocňovanie. Túto akciu je možné vykonať s ľubovoľným číslom. Ľubovoľné číslo umocnené na nulu dá 1 (x 0 = 1).

Nula k ľubovoľnej mocnine sa rovná 0 (0 a \u003d 0).

V tomto prípade okamžite vzniká rozpor: výraz 0 0 nedáva zmysel.

Paradoxy matematiky

To, že delenie nulou je nemožné, vie veľa ľudí zo školy. Ale z nejakého dôvodu nie je možné vysvetliť dôvod takéhoto zákazu. Prečo vlastne neexistuje vzorec delenia nulou, ale iné akcie s týmto číslom sú celkom rozumné a možné? Odpoveď na túto otázku dávajú matematici.

Ide o to, že bežné aritmetické operácie, ktoré sa školáci učia v základných ročníkoch, v skutočnosti ani zďaleka nie sú také rovnaké, ako si myslíme. Všetky jednoduché operácie s číslami možno zredukovať na dve: sčítanie a násobenie. Tieto operácie sú podstatou samotného konceptu čísla a ostatné operácie sú založené na použití týchto dvoch.

Sčítanie a násobenie

Zoberme si štandardný príklad odčítania: 10-2=8. V škole sa uvažuje jednoducho: ak sa z desiatich predmetov odoberú dva, zostane osem. Ale matematici sa na túto operáciu pozerajú celkom inak. Koniec koncov, neexistuje pre nich taká operácia ako odčítanie. Tento príklad možno napísať aj inak: x+2=10. Pre matematikov je neznámym rozdielom jednoducho číslo, ktoré treba pripočítať k dvom, aby vzniklo osem. A tu nie je potrebné žiadne odčítanie, stačí nájsť vhodnú číselnú hodnotu.

Násobenie a delenie sa rieši rovnakým spôsobom. V príklade 12:4=3 sa dá pochopiť, že hovoríme o rozdelení ôsmich predmetov na dve rovnaké kôpky. Ale v skutočnosti je to len obrátený vzorec na písanie 3x4 \u003d 12. Takéto príklady na delenie môžu byť uvedené donekonečna.

Príklady na delenie 0

Tu je trochu jasné, prečo nie je možné deliť nulou. Násobenie a delenie nulou má svoje pravidlá. Všetky príklady na rozdelenie tejto veličiny môžu byť formulované ako 6:0=x. Ale toto je obrátené vyjadrenie výrazu 6 * x = 0. Ale, ako viete, akékoľvek číslo vynásobené 0 dáva v súčine iba 0. Táto vlastnosť je vlastná samotnému konceptu nulovej hodnoty.

Ukazuje sa, že také číslo, ktoré po vynásobení 0 dáva akúkoľvek hmatateľnú hodnotu, neexistuje, to znamená, že tento problém nemá riešenie. Takejto odpovede by sa človek nemal báť, je to prirodzená odpoveď na problémy tohto typu. Len písať 6:0 nedáva žiadny zmysel a ani to nemôže nič vysvetliť. Tento výraz možno v skratke vysvetliť nesmrteľným „bez delenia nulou“.

Existuje operácia 0:0? Skutočne, ak je operácia násobenia 0 legálna, možno nulu deliť nulou? Koniec koncov, rovnica v tvare 0x5=0 je celkom legálna. Namiesto čísla 5 môžete zadať 0, z toho sa produkt nezmení.

Skutočne, 0x0=0. Ale stále nemôžete deliť 0. Ako už bolo povedané, delenie je len opakom násobenia. Ak teda v príklade 0x5=0 potrebujete určiť druhý faktor, dostaneme 0x0=5. Alebo 10. Alebo nekonečno. Delenie nekonečna nulou – ako sa vám páči?

Ale ak sa do výrazu zmestí akékoľvek číslo, tak to nedáva zmysel, nemôžeme si vybrať jedno z nekonečnej množiny čísel. A ak áno, znamená to, že výraz 0:0 nedáva zmysel. Ukazuje sa, že ani nulu samotnú nemožno deliť nulou.

vyššia matematika

Delenie nulou je bolesť hlavy pre stredoškolskú matematiku. Matematická analýza študovaná na technických univerzitách mierne rozširuje koncepciu problémov, ktoré nemajú riešenie. Napríklad k už známemu výrazu 0:0 sa pridávajú nové, ktoré v školských kurzoch matematiky nemajú riešenie:

• nekonečno delené nekonečnom: ∞:∞;
• nekonečno mínus nekonečno: ∞−∞;
• jednotka zvýšená na nekonečnú mocninu: 1 ∞ ;
• nekonečno vynásobené 0: ∞*0;
• niektoré ďalšie.

Nie je možné riešiť takéto výrazy elementárnymi metódami. Ale vyššia matematika vďaka ďalším možnostiam množstva podobných príkladov dáva konečné riešenia. Vidno to najmä pri úvahách o problémoch z teórie limitov.

Zverejnenie neistoty

V teórii limitov je hodnota 0 nahradená podmienenou infinitezimálnou premennou. A skonvertujú sa výrazy, v ktorých sa získa delenie nulou pri dosadení požadovanej hodnoty. Nižšie je uvedený štandardný príklad limitnej expanzie pomocou obvyklých algebraických transformácií:

Ako môžete vidieť na príklade, jednoduché zmenšenie zlomku prináša jeho hodnotu do úplne racionálnej odpovede.

Keď uvažujeme o limitoch goniometrických funkcií, ich vyjadrenia majú tendenciu byť redukované na prvú pozoruhodnú limitu. Pri zvažovaní limitov, v ktorých menovateľ prechádza na 0, keď je limita dosadená, sa používa druhá pozoruhodná limita.

L'Hopitalova metóda

V niektorých prípadoch môžu byť limity výrazov nahradené limitou ich derivátov. Guillaume Lopital - francúzsky matematik, zakladateľ francúzskej školy matematickej analýzy. Dokázal, že limity výrazov sa rovnajú limitom derivátov týchto výrazov. V matematickom zápise je jeho pravidlo nasledovné.

Hlavné elementárne funkcie boli vytriedené.

Pri prechode na funkcie zložitejšej formy sa určite stretneme s výrazmi, ktorých hodnota nie je definovaná. Takéto výrazy sa nazývajú neistoty.

Poďme si všetko vymenovať hlavné typy neistôt: nula delená nulou (0 x 0), nekonečno delené nekonečnom, nula krát nekonečno, nekonečno mínus nekonečno, jedna na mocninu nekonečna, nula na mocninu nuly, nekonečno na mocninu nuly.

VŠETKY OSTATNÉ VYJADRENIA NIE SÚ NEISTOTA A MAJÚ ÚPLNE ŠPECIFICKÚ KONEČNÚ ALEBO NEKONEČNÚ HODNOTU.

Odhaľte neistoty umožňuje:

• zjednodušenie typu funkcie (transformácia výrazu pomocou skrátených násobiacich vzorcov, goniometrických vzorcov, násobenie konjugovanými výrazmi s následnou redukciou a pod.);
• používanie pozoruhodných limitov;
• aplikácia L'Hospitalovho pravidla;
• použitie nahradenia infinitezimálneho výrazu jeho ekvivalentom (pomocou tabuľky ekvivalentných infinitezimálov).

Neistoty zoskupujeme do tabuľka neistoty. Pre každý typ neistoty uvádzame do súladu spôsob jej zverejnenia (metóda hľadania limitu).

Táto tabuľka spolu s tabuľkou limitov základných elementárnych funkcií bude vašim hlavným nástrojom pri hľadaní akýchkoľvek limitov.

Uveďme si pár príkladov, kedy sa po dosadení hodnoty okamžite získa všetko a nevzniká neistota.

Príklad.

Vypočítať limit

Riešenie.

Nahradíme hodnotu:

A hneď sme dostali odpoveď.

odpoveď:

Príklad.

Vypočítať limit

Riešenie.

Do základu našej exponenciálnej mocninnej funkcie dosadíme hodnotu x=0:

To znamená, že limit môže byť prepísaný ako

Teraz sa pozrime na index. Toto je funkcia napájania. Obráťme sa na tabuľku limitov mocninných funkcií so záporným exponentom. Odtiaľ máme a , teda môžeme písať .

Na základe toho môže byť náš limit napísaný ako:

Opäť sa obrátime na tabuľku limitov, ale pre exponenciálne funkcie so základňou väčšou ako jedna, z ktorej máme:

odpoveď:

Pozrime sa na príklady s podrobnými riešeniami odhalenie nejasností transformáciou výrazov.

Veľmi často je potrebné výraz pod medzným znakom mierne transformovať, aby sme sa zbavili nejednoznačností.

Príklad.

Vypočítať limit

Riešenie.

Nahradíme hodnotu:

Došlo k neistote. Pri výbere spôsobu riešenia sa pozrieme na tabuľku neistôt. Skúsme výraz zjednodušiť.

odpoveď:

Príklad.

Vypočítať limit

Riešenie.

Nahradíme hodnotu:

Došlo k neistote (0 x 0). Pozrime sa na tabuľku neistôt, aby sme vybrali metódu riešenia a pokúsili sa zjednodušiť výraz. Čitateľ aj menovateľ vynásobíme výrazom konjugovaný s menovateľom.

Pre menovateľa je prídavný výraz

Vynásobili sme menovateľa, aby sme mohli použiť skrátený vzorec na násobenie - rozdiel druhých mocnín a následne výsledný výraz zmenšiť.

Po sérii premien sa neistota vytratila.

odpoveď:

KOMENTÁR: pre limity tohto druhu je typická metóda násobenia konjugovanými výrazmi, takže ju pokojne použite.

Príklad.

Vypočítať limit

Riešenie.

Nahradíme hodnotu:

Došlo k neistote. Pozrime sa na tabuľku neistôt, aby sme vybrali metódu riešenia a pokúsili sa zjednodušiť výraz. Keďže čitateľ aj menovateľ zaniknú pri x=1, ak je možné tieto výrazy zredukovať (x-1) a neistota zmizne.

Rozložme čitateľa na faktor:

Rozložme menovateľa na faktor:

Náš limit bude mať podobu:

Po premene sa ukázala neistota.

odpoveď:

Zvážte limity v nekonečne mocninných výrazov. Ak sú exponenty exponenciálneho výrazu kladné, potom je limita v nekonečne nekonečná. Navyše, hlavná hodnota má najväčší stupeň, zvyšok môže byť vyradený.

Príklad.

Príklad.

Ak je výraz pod medzným znamienkom zlomok a čitateľ aj menovateľ sú mocninnými výrazmi (m je mocnina čitateľa a n je mocnina menovateľa), potom keď je tvar nekonečno neurčitý v tomto prípade do nekonečna ukazuje sa neistota delenie a čitateľ a menovateľ podľa

Príklad.

Vypočítať limit